Toonladder theorie

Toonladders en toonsoorten

---

De begrippen toonladder en toonsoort zijn nauw met elkaar verwant, maar verwijzen toch naar verschillende zaken. Een toonladder is een gedefinieerde reeks tonen, stijgend of dalend. Normaal gesproken omspant zo’n reeks een octaaf.
De eerste toon van de reeks die dan als octaaf aan het eind terugkeert, is de grondtoon van de toonladder. Meestal worden de noten op een toonladder als een stijgende toonreeks genoteerd.

De voor de gitaar belangrijke toonladders zijn zogeheten diatonische toonladders, dat wil zeggen dat elke volgende toon is afgeleid van de eerstvolgende hogere of lagere stamtoon.
De intervallen tussen de elkaar opvolgende tonen zijn daardoor vrijwel steeds halve of hele tonen (1 fret of 2 fretten op de gitaarhals), ook wel genoemd klein en grote secunden.

Zo’n diatonische toonladder bestaat dan uit zeven opeenvolgende tonen plus de herhaling van de grondtoon. Zo krijg je in totaal weer de 8 tonen van een octaaf.

Een toonsoort is een kenmerk van een muziekstuk, en de toonsoort geeft aan welke toonladder wordt gebruikt. Een muziekstuk in bijvoorbeeld D-groot (D-Majeur of in het Engels "D Major") heeft als toonsoort D-groot of D-grote-terts (in het Engels simpelweg "D"). Er zijn twee verschillende toonladders die veel gebruikt worden, namelijk de majeur (Engels "Major") en de mineur (Engels "Minor") toonladder. Beide toonladders bestaan uit zeven verschillende noten. De achtste noot is weer exact hetzelfde als de eerste, zoals we zojuist al uitgelegd hebben. Het grootste verschil tussen beide toonladders voor het gehoor, is dat een majeur toonladder als vrolijk klinkend wordt beschouwd, en een mineur toonladder als droevig. Daarnaast verschillen de toonafstanden bij de toonladders, daarop komen we later nog terug.

We geven als voorbeeld de C Majeur (C Major) toonladder. De tonen van de C-majeur toonladder zijn C – D – E – F – G – A – B – C, en dat ziet er in muziekschrift als volgt uit:

Hieronder zie je waar je deze zeven tonen kunt vinden op een piano toetsenbord en gitaar.

In de Westerse muziek kennen we twaalf verschillende tonen. Maar kijk je naar een piano, dan zie je er véél meer dan twaalf. Dit komt omdat die twaalf tonen steeds herhaald worden. Deze twaalf tonen hebben namen, die je in de afbeelding hierboven ziet.
Tussen elk van de twaalf tonen zit steeds dezelfde toonsafstand: een halve toon, of om in gitaartermen te blijven, 1 fret op de gitaarhals.
Twee halve tonen bij elkaar is dan een hele toon. Van C naar C♯/D♭ wordt dus een halve toon genoemd, van C naar D een hele toon, van C naar D♯/E♭ anderhalve toon, enzovoorts.

Een toonladder is een rijtje van bijvoorbeeld zeven tonen. We gebruiken dus niet alle twaalf mogelijkheden. Deze tonen kunnen de basis vormen voor een liedje of compositie. Natuurlijk kun je als componist of liedjesschrijver daarvan afwijken, maar de gekozen toonladder blijft altijd de kapstok voor het muziekstuk. Een van de meest gebruikte toonladders is de majeur-toonladder, ook wel grote terts-toonladder genoemd.

Majeur toonladders

---

Majeur toonladders bestaan uit zeven noten (voordat de toonladder een octaaf hoger opnieuw begint, zoals we geleerd hebben), en bestaat uit een speciale volgorde van halve stappen (twee noten die direct aan elkaar grenzen) en hele stappen (noten die twee halve stappen van elkaar verwijderd zijn).
Dit specifieke patroon van hele stappen en halve stappen bepaalt dat het een majeur toonladder is, ongeacht op welke noot je begint. De afbeelding hiernaast laat dat zien. Tussen C + D zit een hele stap (1) omdat er één zwarte toets tussen zit. Tussen E + F zit een halve stap (½) omdat er géén zwarte toets tussen zit, dus:

Op de gitaar is een halve stap (½) gelijk aan één fret opschuiven, een hele stap (1) is gelijk aan twee frets opschuiven. Zou je de toonladder van F op een gitaarhals maken via de 6^e snaar, de lage-E snaar, dan ziet dat er dan zoals in de afbeelding hiernaast.
Het voordeel van een gitaar is dat dezelfde noten veelvuldig op andere plaatsen van de hals voorkomen, we zouden dus bijvoorbeeld de A op de vijfde positie naar de open A snaar kunnen verplaatsen, omdat ze precies hetzelfde klinken.
Alle andere noten vanaf A (dus B♭, C, D, E en F) verschuiven dan ook naar de open A snaar (de vijfde snaar).

De noot D op de A-snaar is dezelfde noot als de open D-snaar (de 4de snaar). Je kunt dus alle noten vanaf positie 5 op de A-snaar, verschuiven naar de open D-snaar. Daardoor verschuiven ook de noten na D, dus E en F, naar de D-snaar.
Je pakt als het ware alle te verschuiven noten op en plaatst ze op een passende plek op de hals weer terug. De toonafstanden (1   1   ½   1   1   1   ½) blijven altijd gelijk, ook met het verplaatsen van (delen van) een toonladder. Onderstaande illustraties laten dit verschuivingsproces zien.

Verschuiven noten uit de F toonladder van de lage E-snaar de A-snaar

Verschuiven noten uit de F toonladder van de A-snaar de D-snaar

Het prachtige van gitaar is dat als je eenmaal zoals bovenstaand een toonladder hebt gevonden, in ons voorbeeld een F toonladder, is dat je de hele toonladder als het ware kunt oppakken om bijvoorbeeld een G-toonladder te maken, en daarvoor moet je de hele toonladder twee frets (één hele stap), opschuiven.

Zonder dat je nu de namen van de noten uit de G-toonladder kent, heb je van de F-toonladder een G-toonladder gemaakt.

De noten uit de F-toonladder zijn: F   G   A   B♭   C   D   E   F.


Door deze één stap (2 frets) op te schuiven is het de G-toonladder geworden met de noten: G   A   B   C   DE   F♯   G.

Zo kun je de "shape" (de vorm) van de toonladder nog eens één hele stap opschuiven, en je gaat van de G-toonladder naar de A-toonladder, met de noten:
A   B   C♯   D   E   F♯   G♯   A.



Je kunt vanuit deze positie zelfs de vorm ("shape") een snaar naar beneden verplaatsen, dus van de 5^e positie van de E-snaar naar de 5^e positie van de A-snaar, en daarmee ben je aanbelandt in de D-toonladder met de noten: D   E   F♯   G   A   B   C♯   D.

Nog verder opschuiven naar beneden (dus van de A-snaar de D-snaar) gaat niet, omdat (uitsluitend) op de B-snaar, waar dan het "onderste" rijtje noten terechtkomt, de intervallen anders zijn. Het begrip intervallen komen we nog op terug.
Je kunt hiervan onthouden dat deze vorm ("shape") altijd een Majeur toonladder oplevert.

Als je naar de noten op de gitaarhals kijkt, dan zie je waarom de B-snaar (de 2^e snaar), een wat "rare" interval heeft.

Alle snaren gaan met hun noten van de 5^e positie naar de daaropvolgende open-snaar positie, behalve bij de B-snaar, die heeft dezelfde klinkende noot "B" van de G-snaar, op de 4^e positie staan. Daarom kan de majeur toonladder vorm niet helemaal van "boven" naar "beneden" over de hals worden geschoven.


We hebben 12 noten in een octaaf zitten, kijk eens naar de afbeelding hiernaast, van de lage-E snaar op je gitaar. Te beginnen met de stamtoon E (open snaar) schuiven we 12 posities op (12 maal een halve toon) de gitaarhals verder om de geoctaveerde E te bereiken. Je begrijpt nu ook waarom op de 12^e fret twee puntjes op de gitaarhals staan, in plaats van één puntje op de frets 3, 5, 7, 9, 15, 17, 19 en 21. De twee puntjes geven aan waar het octaaf van de open snaren eindigt.
Als je deze logica voor iedere snaar volgt, dan heb je op de 12^e fret dezelfde notenvolgorde als bij de open snaren (E, A, D, G, B, e), alleen een octaaf hoger.

Je hebt geleerd dat het schema van een majeur toonladder bestaat uit het volgende "stappenplan": 1   1   ½   1   1   1   ½.
Daarmee kun je iedere toonladder als het ware "uitrekenen". In onderstaande tabellen geven we je de majeur toonladders met alle kruizen en mollen (♯ en ♭).

Mineur toonladders

---

De majeur-toonladder heeft het volgende stappenplan: 1   1   ½   1   1   1   ½.
Neem je als voorbeeld een G majeur toonladder, dan krijg je: G   A   B   C   D   E   F♯   G.
Het stappenplan van de mineur-toonladder is afwijkend, en is als volgt: 1   ½   1   1   ½   1   1.

Nemen we als ander voorbeeld een C Mineur toonladder, dan ziet er dat in notenschrift, op het piano toetsenbord en de gitaarhals als volgt uit:

Je kunt gebruikmaken van het mineur stappenplan, dus 1   ½   1   1   ½   1   1,een andere mogelijkheid is om vanuit de majeur toonladders te bepalen welke mineur toonladder erbij hoort. Daarmee vind je ook iedere mineur toonladder. Dus stel dat je de theorie over de majeur toonladders volledig in je hoofd hebt zitten, dan kun je vandaar uit de bij elke majeur toonladder de bijbehorende mineur toonladder bepalen.

Parallelle toonladders

Eerst leggen we even het begrip "natuurlijke" mineur toonladder uit. Waarom praten we over "natuurlijke" mineur toonladders, we noemden de majeur toonladders toch ook niet natuurlijk?
We doen dit omdat er maar één soort majeur toonladder is, maar er bestaan drie verschillende soorten mineur toonladders, te weten:

• Natuurlijke mineur toonladders
• Harmonische mineur toonladders
• Melodische mineur toonladders

In de muziektheorie heten de twee toonaarden of toonsoorten in majeur en mineur met dezelfde voortekening parallelle toonaarden of je zegt, ze zijn van een paralleltoonaard. Dezelfde voortekening wil zeggen dat de majeur en de mineur toonladder dezelfde hoeveelheid kruizen (♯) of mollen (♭) hebben. Een weetje daarbij is, is dat de parallelle mineur toonladder loopt van de 6^e tot de 6^e toon. Laten we dit eens uitzoeken voor de parallele mineur toonladder van de C majeur toonladder.

Als we de C majeur toonladder nu eens in een cirkel zetten, zoals hiernaast, en we geven er bij aan op welke plaats de noot in de toonladder staat, zoals je ziet, dus: C = 1, D = 2, E = 3, F = 4, etc.
Tussen de verschillende noten staat het stappenplan van de majeur toonladder, dus: tussen C en D = 1 stap, tussen D en E is 1 stap, tussen E en F is ½ stap, etc.
Als we nu zeggen dat de parallelle mineur toonladder op de 6 plaats begint van de majeur toonladder, dan is het duidelijk dat de A mineur toonladder de parallelle toonladder is van de C majeur toonladder.
De C majeur toonladder heeft geen voortekens zoals we weten, dus ook de parallelle A mineur toonladder heeft dan geen voortekens.

We geven een tweede voorbeeld, nu vanuit de B majeur toonladder. Als we de noten van de toonladder in de cirkel plaatsen, en we houden rekening met de onderlinge afstanden, het "stappenplan" van de majeur toonladder, dan krijgen we de afbeelding hiernaast.
De 6^e toon van de B majeur toonladder is de G♯, dus de parallelle mineur toonladder van B majeur is G♯ mineur.

De B majeur toonladder heeft vijf voortekens, dus de parallelle G♯ mineur toonladder zal ook vijf voortekens krijgen. Volgen we nu het stappenplan van de mineur toonladder (1   ½   1   1   ½   1   1), dan komt een en ander er als volgt uit te zien:

Let op! We hadden in de G mineur toonladder bijvoorbeeld ook kunnen schrijven B♭ in plaats van A♯, en D♭ in plaats van C♯ (of in plaats van de F♯ een G♭), en dan hadden we de volgende noten in de toonladder verwerkt: G♯   B♭   B   D♭   D♯   E   G♭   G♯  
Op de gitaar klinkt een A♯ immers hetzelfde als een B♭, een D♭ hetzelfde als een C♯, en een F♯ hetzelfde als een G♭.
De afspraak is echter dat alle acht tonen moeten voorkomen in het octaaf, en door een B♭, D♭ en G♭ te schrijven, missen we de noten A, C en F. Daarom moeten we in dit geval de noten A, C en F met een halve toon verhogen, en er een A♯, C♯ en F♯ van maken. Dan hebben we in ieder geval weer alle tonen in de toonladder zitten.

We hebben bij de majeur akkoorden gezien, dat je de toonladdervorm ("shape") over de hals van de gitaar kunt bewegen, om van het ene akkoord in het andere over te gaan. Dat werkt bij mineur toonladdervormen precies hetzelfde.

Het klankverschil tussen majeur en mineur

We hebben het al gezegd: een toonladder bepaalt de sfeer van de muziek. Onderstaand een tweetal geluidsfragmenten, het meest linkse geluidsfragment is een oplopende C majeur toonladder, het tweede geluidsfragment is een oplopende C mineur toonladder.

   

Het verschil zul je wel horen. De majeur toonladder klinkt vrolijker en meer opgewekt, de mineur toonladder klinkt wat triester, tragischer of melancholiser. Onthoud altijd: niet alleen majeur en mineur bepalen hoe vrolijk of droevig een nummer klinkt. Ook ritme, tempo, dynamiek en de gebruikte instrumenten hebben hier invloed op. Zo wordt langzame, zachte muziek eerder als droevig ervaren, terwijl "upbeat", harde muziek vaker als vrolijk wordt ervaren.

De leidtoon

Een belangrijk onderscheid tussen majeur en mineur toonladders wordt door het gebruik van een zogeheten "leidtoon" bepaald. In de majeurtoonladder is dit de zevende toon, bijvoorbeeld in in C-majeur de toon B. Deze toon heet de leidtoon, omdat die toon voor je gevoel heel sterk naar de volgende toon wil: je wordt bijna gedwóngen om de volgende toon te spelen.
Probeer maar eens de toonladder van C majeur te spelen, maar dan zonder de laatste C. Je zal dan wel aanvoelen dat er nog een toon na die B móet komen, anders klinkt het als een verhaal met een open eind.

De mineur-toonladder heeft deze leidtoon trouwens niet. Die zevende toon van de mineur-toonladder (dat is de B♭ in het c mineur-voorbeeld) heeft veel minder sterk de neiging om naar de laatste toon te gaan.
Omdat componisten dit toch wel een gemis vonden, zijn ze in de loop der tijden deze laatste, hele stap van de mineurtoonladder in veel gevallen toch maar gaan wijzigen naar een halve stap. Het resultaat heet de harmonische mineurtoonladder, zie het verschil:

C mineur natuurlijk	C	D	E♭	F	G	A♭	B♭	C
C mineur harmonisch	C	D	E♭	F	G	A♭	B	C

Naam toonladder	Begintoets	Noten toonladder	Gebruikt in ...
Ionisch	C	C   D   E   F   G   A   B   C	Country & Western, kinderliedjes, pop, jazz
Dorisch	D	D   E   F   G   A   B   C   D	Pop, jazz, (symfonische) rock
Frygisch	E	E   F   G   A   B   C   D   E	Flamenco
Lydisch	F	F   G   A   B   C   D   E   F	Filmmuziek (heeft een wat dreigende klank)
Mixolydisch	G	G   A   B   C   D   E   F   G	Blues, soul, jazz
Aeolisch	A	A   B   C   D   E   F   G   A	Standaard mineur toonladder
Locrisch	B	B   C   D   E   F   G   A   B	Jazz (met verminderde akkoorden)

Intervallen en harmonie

---

Bij veel cursussen muziektheorie is de kwintencirkel een van de eerste zaken die behandeld wordt. Dat is wat merkwaardig, omdat je al veel moet weten om iets van de kwintencirkel te kunnen begrijpen. We gaan er vanuit dat je in ieder geval het website-onderdeel "Basis muziektheorie" hebt bestudeerd.
Voor de zekerheid geven we nog de theorie van de webpagina "Akkoordentheorie", het onderdeel "Intervallen en harmonie". Mocht je dat al bestudeerd hebben, dan kun je deze paragraaf overslaan en direct aan de volgende paragraaf beginnen, die over de kwintencirkel gaat.

De naamgeving van akkoorden is gebaseerd op de grondnoot of grondtoon van het akkoord. In het Engels heet deze grondnoot of grondtoon een "root note".
Een D Majeur akkoord (in het engels een "D Major") heeft zijn naam gekregen omdat de grondtoon van het akkoord een D is. Overigens wordt een D Majeur akkoord ook wel een D Grote Terts genoemd.

Voordat we kunnen uitleggen hoe akkoorden opgebouwd worden en waarom die grondtoon ("root") zo belangrijk is, moeten we eerst door wat taaie muziektheorie heen, met name om de begrippen prime, terts en kwint te snappen, die extreem belangrijk zijn bij het bouwen van akkoorden.

Prime, terts en kwint zijn de basisingrediënten van bijna elk akkoord. Een akkoord bestaat uit minimaal drie verschillende tonen die tegelijk klinken. De begrippen prime, terts en kwint hebben te maken met toonsafstanden, waarbij we, ter herinnering, noemen dat er in totaal twaalf tonen in de Westerse muziek bestaan, waarvan er zeven stamtonen worden genoemd.

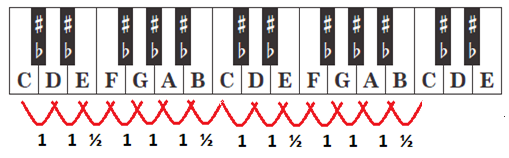
Aan de hand van het piano toetsenbord hiernaast, zien we de 7 stamtonen die we kennen: C, D, E, F, G, A en B (daarna beginnen we weer met C). Uitgebreide informatie hierover vind je onder de menu optie "Muziekleer", we volstaan hier met te melden dat er hele stappen tussen twee stamtonen zitten (aangeduid met 1), als er een zwarte toets tussen zit. Als er geen zwarte toets tussen twee tonen zit, bijvoorbeeld van E naar F en van B naar C, dan is er sprake van een ½ stap.

Op je gitaarhals is iedere fret een ½ stap,dus ga je van een C naar een D, dan zit daar volgens het piano toetsenbord een C♯/D♭ toon tussen, dus moet je 1 hele stap (C naar C♯/D♭ is ½ stap + C♯/D♭ naar D is ½ stap), oftewel 2 frets op je gitaar opschuiven.



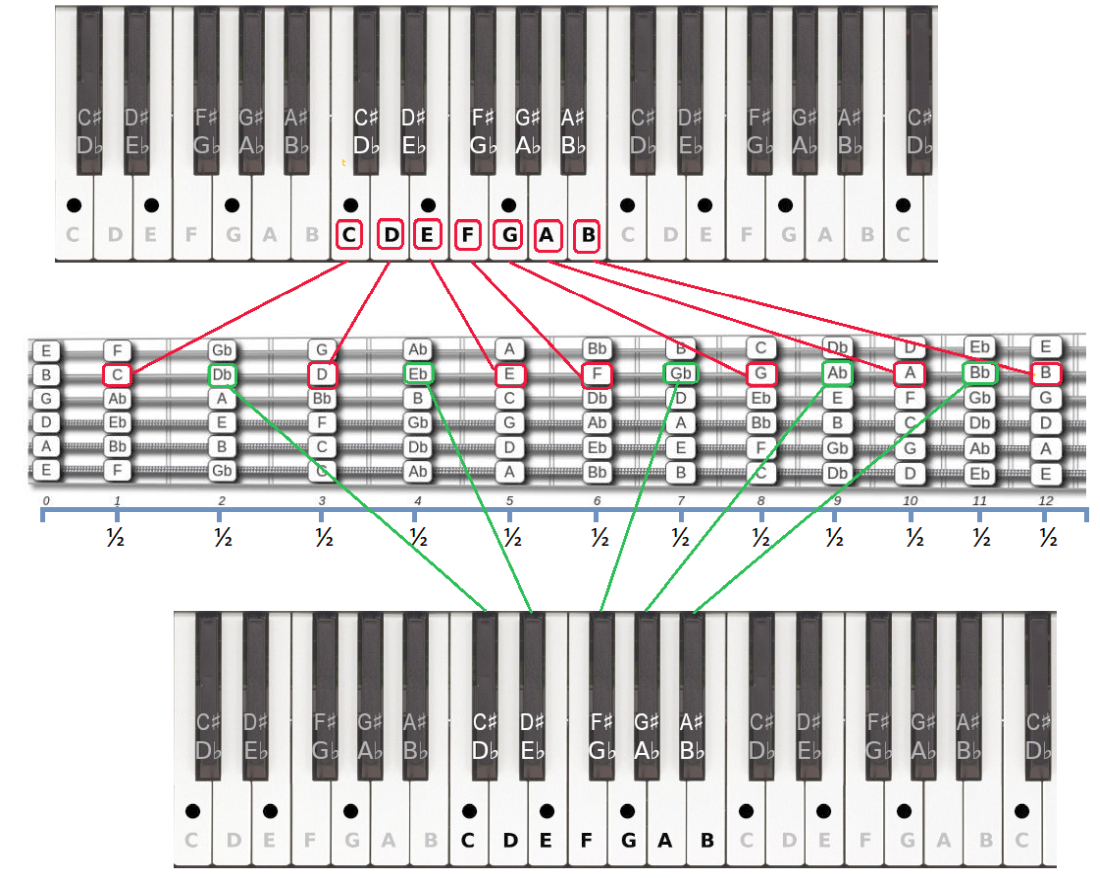
De illustratie hierboven laat zien op welke manier je de stamtonen vanaf een piano toetsenbord koppelt aan de hals van een gitaar. We hebben in dit voorbeeld de C toon genomen die op de B snaar, eerste fret, begint. We hadden iedere andere C op de hals als uitgangspunt kunnen nemen, bijvoorbeeld ook de C toon op de 8^ste fret van de lage E snaar, of de C toon op 3^e fret van de A snaar.
De 7 stamtonen vanaf het piano toetsenbord naar de gitaarhals zijn met rode lijnen gekoppeld, de tussenliggende halve tonen zijn door middel van een groene lijn gekoppeld. De blauwe cijferbalk laat zien dat iedere fret exact een ½ stap verschuiving van een toon is. Even een klein wetenswaardigheidje:
Als je van het begin van de gitaarhals naar boven telt, dus van fret 0 naar fret 22, is iedere halve noot een "is" noot (spreek uit: "ies"), in het Engels een "sharp". Ga je van fret 22 terug naar fret 0, dan is iedere halve noot een "es", in het Engels een "flat".
Het notatieteken voor een "is" is ♯
Het notatieteken voor een "bes" is ♭
Soms zie je een teken achter de stamtoon, om aan te duiden dat het geen "is" of een "bes" is, en dat teken ziet er zó uit: ♮. Dit is de aanduiding voor een natuurlijke toon, in het Engels "natural".

In een tabel ziet dit er als volgt uit (we nemen alle twaalf de tonen, dus de stam- en halve of tussentonen). Het uitgangspunt is de eerste C die we tegenkomen op de B snaar, net zoals in het voorbeeld hierboven met het koppelen van het piano toetsenbord aan de frets op de gitaarhals. In de tweede kolom zie je de noot die bij een bepaalde fret op de B snaar hoort.
De kolommen "Frets →" en "Frets ←" hebben we in de tabel verwerkt zodat je ziet, hoe de toon op een bepaalde fret genoemd wordt, als je aan het tellen bent van fret 0 (gitaarhals) naar fret 22, of omgekeerd, als je van fret 22 terugtelt naar 0.
Dus: zit je op fret 5 en tel je terug naar fret 4, dan heet de noot op fret 4 een E♭ (Es), tel je van fret 3 naar fret 4 (dus omhoog op de hals), dan heet de noot een D♯ (Dis).
Verder is bij iedere noot zowel de Nederlandse als de Engelse schrijfwijze en uitspraak gegeven, waarbij het werken met de notatiesymbolen ♯ en ♭, de voorkeur verdient als je akkoorden gaat opschrijven.

Als je duidelijk is, hoe de logica van je gitaarhals qua noten in elkaar steekt (zie anders nog even bovenstaande afbeeldingen), dan komen we nu tot de volgende stap in de theorie van het naamgeven van akkoorden.
Tussen twee stamtonen zit natuurlijk een bepaalde toonsafstand. Voor elk zo’n interval hebben we een naam. De afstand tussen een stamtoon en de eerstvolgende stamtoon heet een secunde (zoals van C naar D, of van E naar F). Ofwel, tel je twee letters, dan heb je een secunde. De afstand van C naar E is drie letters (C – D – E) en heet een terts. Vier letters is een kwart (C naar F). Hieronder vind je alle belangrijke intervalnamen, met de Engelse benamingen:

Grote en kleine terts

Net als van C naar E, wordt bijvoorbeeld ook van E naar G een terts genoemd. Je telt immers drie letters (E – F – G).
Hier is iets vreemds mee aan de hand. Want de afstand E – G is kleiner dan de afstand C – E. Kijk naar de afbeelding van de pianotoetsen en tel de halve tonen. Tussen C en E zitten vier halve tonen, maar tussen E en G drie halve tonen.

Van C naar E (vier halve tonen) noemen we een grote terts, van E naar G (drie halve tonen) een kleine terts.

Ook de septiem heeft een grote en kleine variant. De afstand C – B is een septiem (zeven letters), net als de afstand D – C (zeven letters). Tussen C en B zitten echter elf halve tonen (een grote septiem), terwijl er tussen D en C tien zitten (kleine septiem).
Zo zijn er verder nog de grote en kleine secundes, en grote en kleine sexten. Hieronder meer daarover.

Een belangrijke Opmerking: als je op de C begint en je wilt een kleine septiem maken in plaats van een grote septiem, maak je van de B een B♭. Het is niet de bedoeling dat je de A verhoogt naar een A♯.
Ja, theoretisch is het dezelfde afstand (tien halve tonen), maar het is erg verwarrend voor de muzikant!
De afstand tussen de letters C – A is namelijk een sext (zes letters), en geen septiem (zeven letters).
Kortom, je telt eerst de letters. Als het nodig is, verhoog of verlaag je daarna de toon om hem "klein" of "groot" te maken (zonder daarbij van letter te veranderen).

De belangrijkste intervallen

We zetten de belangrijkste intervallen op een rijtje, met de tonen C en A als voorbeeld-grondtonen. En denk eraan: je telt eerst de letters. Als het nodig is, verhoog of verlaag je daarna de toon om hem groot of klein te maken (zonder daarbij van letter te veranderen).
Gebruik het pianotoetsenbord of de gitaarhals bovenaan deze paragraaf om het aantal halve tonen te tellen.
Elk van de intervallen heeft een eigen klank. Door er heel veel mee te werken, zul je ze langzaam maar zeker leren herkennen.

Belangrijke opmerking: Als je een noot ziet met bijvoorbeeld twee mollen (♭♭), dan is die noot extra verlaagd met nóg een halve toon. Bij de B♭♭ bijvoorbeeld, zoals je die hierboven in de tabel ziet, speel je daardoor in de praktijk een A.

Samenhang piano toetsenbord en gitaarhals

We hebben hiervoor al duidelijk gemaakt, dat er een samenhang bestaat tussen een toetsinstrument (piano) en de (elektrische) gitaar. Kijk nog maar eens naar de theorie over toonladders en toonsoorten hierboven, waarbij we de witte en zwarte toetsen hebben "vertaald" naar posities op de gitaarhals. Als je zelf muziek gaat componeren, is het handig om voor alle posities op je gitaar te weten, welke witte en zwarte toetsen op de piano met de gitaarhalsposities corresponderen. Dan weet je zeker dat je muziek tonaal blijft, en de gitaar en de toetsen prima met elkaar in harmonie-evenwicht zijn. Met tonaal bedoelen we in dit geval dat er een prettig samenklinkende harmonie en melodie tussen alle instrumenten in een muziekstuk bestaat, binnen ons Westerse toonsysteem. Daardoor neem je als luisteraar automatisch de structuur van een muziekstuk tot je, en voldoet het muziekstuk aan je gehoormatige verwachtingen.
Tonale muziek verloopt vaak volgens de regels van de klassieke harmonieleer. Als je daarover meer wilt weten, lees dan onze website module MUZIEKTHEORIE | HARMONIELEER.

Marcel Ellenbroek uit Zwolle (musicus en componist) heeft voor dit soort compositorische vraagstukken een "positiekaart" ontwikkeld, die de relatie tussen de pianotoetsen en de gitaarhals duidelijk weergeeft.

Hetzelfde principe kun je voor een 4-snarige basgitaar toepassen. Omdat we voor de basgitaar-module op de website geen aparte muziektheorie hebben geïntroduceerd (de theorie is immers voor iedere gitaar gelijk), geven we je tevens de "positiekaart" voor de basgitaar.

De kwintencirkel

---

De kwintencirkel is een soort "rekentool" en wordt onder andere gebruikt om te bepalen of een toonladder met kruizen of mollen genoteerd moet worden, en hoeveel kruizen of mollen er in die toonladder voorkomen.
De kwintencirkel is een opeenvolging van tonen of toonaarden, voorgesteld als een cirkel, waarbij iedere volgende stap op de cirkel zeven halve noten hoger ligt dan de vorige.

De kwintencirkel gaat dus niet op alfabetische volgorde, de volgende majeur toonladder wordt altijd gevonden door uit de vorige toonladder de reine kwint (perfect 5^th) noot te pakken, dus in de toonladder van C ga je naar G, vanuit G ga je naar D, etc.
De truc is, als je naar de volgende majeur toonladder in de reine kwint gaat, moet je altijd de 7^e noot van die volgende toonladder verhogen, en de rest van de verhogingen laten zoals deze zijn. Dan heb je de volgende toonladder te pakken, dus:

Vanaf C (de bovenkant van de kwintencirkel)kun je ook tegen de klok in. Hierbij krijgt elke volgende toonladder een mol aan de sleutel extra. Toonladder F heeft 1 mol. Toonladder B♭ heeft 2 mollen.
Om toonladders rechts van het C majeur akkoord te bepalen, kun je een reine kwart (perfect 4^th) van links naar rechts opzoeken, of een reine kwint (perfect 5^th), van rechts naar links. We laten dat aan de hand van een voorbeeld zien, waar we vanuit de C van de bovenkant naar de eerstvolgende toonladder willen, maar dan tegen de klokrichting in.

In de afbeelding hiernaast zie je de toonladder van C. Je ziet beide manieren waarop je kunt bepalen wat de toonladder tegen op de kwintencirkel, tegen de klokrichting in, zal zijn.

Door vanaf de laatste C in het octaaf een reine kwint (7 halve stappen) terug te tellen, kom je bij de F uit.
Tel je vanaf de eerste C in het octaaf een reine kwart naar rechts (5 halve stappen), dan kom je ook bij de F uit.

Zo kun je weer een tabel maken:

Aan de onderkant van de cirkel vindt er een overlapping plaats. Dit noemen we enharmonisch gelijke toonsoorten.
Als je goed kijkt naar de kwintencirkel hieronder, dan zie je dat aan de buitenkant, met rode letters, de majeur toonladders staan, en aan de binnenkant van de cirkel, in groene letters, de mineur toonladders.
Bij iedere majeur toonladder staat de parallelle toonladder in mineur, en ongekeerd. C majeur is de parallelle toonladder van A mineur, en omgekeerd.

Transponeren van toonladders en akkoorden

---

In muziek wordt de term transponeren of transpositie gebruikt om aan te geven dat een muziekstuk in een nieuwe toonsoort geschreven wordt. Transponeren komt er in feite op neer dat iedere noot van de originele compositie met hetzelfde aantal halve tonen of hele tonen wordt verhoogd of verlaagd. Op sommige instrumenten kunnen niet zomaar alle toonladders moeiteloos gespeeld worden, en dan is het handig een bij het instrument passende toonladder voor de musicus te gebruiken.

Enkele voorbeelden (zie tevens de kwintencirkel uit de vorige paragraaf):
Transponeren van C naar C♯/D♭: alles een halve toon hoger (7 kruisen/5 mollen erbij)
Transponeren van C naar D: alles een hele toon hoger (2 kruisen erbij)
Transponeren van D naar C: alles een hele toon lager (2 kruisen eraf)

Als je meegekeken hebt via de kwintencirkel, dan zie je hoe gemakkelijk je met de kwintencirkel van de ene naar de andere toonladder kunt transponeren. Je ziet in één oogopslag wat in de nieuwe toonladder de voortekens (♯ of ♭) moeten zijn.

Transponeren van akkoorden

Transponeren kan niet alleen met toonladders, maar ook met de akkoorden die tot de toonladder behoren. Daarvoor introduceren we nu het verschijnsel toontrappen, die je een beetje kunt beschouwen als de "treden" van een toonladder. Als je overigens meer van (gitaar) akkoorden wilt weten, kijk dan bij de menu opties "Akkoorden theorie" en "Akkoorden diagrammen" van deze website.
Daarvoor kunnen we iedere toon in een toonladder een nummer geven, en wel van 1 tot en met 8. De cijfers die we daarbij gebruiken zijn romeinse cijfers, zoals van oudsher in de muzieknotatie gebruikelijk is. Laten we eens samenvatten wat we tot nu toe uit de basis muziek- en toonladdertheorie hebben geleerd:

We zien in deze notenbalk de intervallen zoals we die geleerd hebben, dus prime, secunde, terts, kwart etc. We hebben de noten die bij de intervallen horen, op de notenbalk geplaatst.
Bij de terts betekent dit bijvoorbeeld, dat de toonsafstand tussen de prime en de terts 1½ of 2 tonen is, afhankelijk van het feit of er sprake is van een kleine of een grote terts. Op de notenbalk zie je bij ieder interval de prime (als een C noot aangegeven) en de noot van het interval, in het geval van de terts de noot op E. Bij de kwint is dat de noot op G, enzovoorts. Dan snap je wat de onderlinge verhouding tussen die noten is.

Onder de notenbalk zie je de toontrappen staan, met Romeinse cijfers en met een bijpassende naam. Het schema van de toontrappen in tabelvorm is als volgt, waarbij we de toonladder in C als voorbeeld gebruiken:

Als je goed hebt opgelet, dan heb je gezien dat een aantal Romeinse cijfers in kleine cijfers zijn, de ii, iii, vi en vii.
Dat is niet zonder reden. De kleine cijfers geven aan dit deze noot, als die naar een akkoord wordt omgezet, een mineur akkoord moet zijn.

Op iedere toon I tot en met vii (I), plaatsen we een akkoord, en wel een drieklank. Dit zijn de basisakkoorden die bij de toonladder horen. Voor de toonladder in C zijn de basisakkoorden dus als volgt:
I = C, ii = Dm, iii = Em, IV = F, V = G, vi = Am, vii = B^dim, en tenslotte weer een C.

Onder een toontrap verstaan we dus het rangcijfer van de toon in die toonladder, maar ook het akkoord wat op deze toon is geplaatst. Trap IV van de toonladder van C is de F, en het bijbehorende akkoord op trap IV is daarom het F-akkoord.

De onderste toon van een akkoord heet de grondtoon. Meestal gebruiken we de grondtonen als bastoon van een akkoord, dit is de laagste toon van het akkoord, maar het kan soms ook anders. In de afbeelding hiernaast zie je het C akkoord zoals je dat op de gitaarhals plaats, de laagste toon van het akkoord is een C, op de 5^e snaar, 3^e fret.
De 6e snaar, de lage E-snaar, speel je niet, er staat in het akkoorddiagram immers een kruis bij deze snaar.
De tonen waaruit het C akkoord voor gitaar is opgebouwd zijn: C, E, G, C en E. Dat zijn strikt genomen meer tonen dan je in een drieklank nodig hebt. Maar omdat het op de gitaar heel mooi klinkt om de extra C en E toon in het akkoord te betrekken (het akkoord klinkt dan voller), is het C akkoord iets uitgebreid.

We kunnen in ieder geval stellen dat een majeurakkoord (oftewel een grote drieklank) gevonden wordt op de trappen I, IV en V van de toonladder. Een mineurakkoord ofwel een kleine drieklank vinden we op de trappen ii, ii en vi.
De drieklank op trap vii heet verminderde drieklank ("diminished"), omdat deze is opgebouwd uit twee kleine tertsen die op elkaar worden gestapeld.

Een belangrijke regel uit de muziekgeschiedenis is, dat de dominant graag wil oplossen naar de tonica (in ons toonladder C voorbeeld van de G naar de C), en de onderdominant wil graag voorafgaan aan de dominant (in ons voorbeeld zou de F voorafgegaan aan de G).
In het voorbeeld van de G naar de C betekent dit, dat de grondtoon van het G akkoord (de G), verandert naar de grondtoon van het C akkoord (de C).

Een dominanten-ketting is een opeenvolging van akkoorden die telkens de functie van dominant en tonica hebben.
Zo'n dominanten-ketting klinkt erg mooi en maakt eigenlijk de perfecte harmonische verbinding. Maar wanneer we dit te lang volhouden wordt het erg saai. Daarom klinkt er in diverse muziekstijlen, van klassiek tot pop, heel vaak een klein stukje van zo'n dominantenketting en dat is bijzonder mooi.

Nu duidelijk is hoe de kwintencirkel en toontrappen in elkaar steken, is het niet zo moeilijk meer om akkoorden te transponeren.
De eerste belangrijke stap is het achterhalen van de oorspronkelijke toonsoort van de song die je wilt transponeren. Veel muziekstukken beginnen en eindigen op het akkoord van de gebruikte toonladder, zij het dat daarop nogal eens enige uitzonderingen zijn. Enkele voorbeelden:
Als de akkoordprogressie van een song is C F G, dan is de toonsoort C
Een song met de akkoordprogressie G Em Bm D zal naar alle waarschijnlijkheid in de toonsoort G staan
Een song met de akkoorden F B♭ C, zal in F staan.

Transponeren met toontrappen en de kwintencirkel

Stel dat we een akkoordenprogressie in de C toonladder hebben, dat er als volgt uitziet: C F Am G.
Uitgaande van diezelfde toonladder in C, gaan we nu de Romeinse cijfers (de toontrappen), bij de akkoorden plaatsen.

We vullen het akkoordenschema met de toontrappen aan, omdat het dan gemakkelijker wordt de akkoordenprogressie om te zetten naar een andere toonsoort. We hebben de akkoorden C, F, Am en G, met de toontrappen erbij hebben we dan:

We gaan nu de akkoordprogressie uit de toonsoort C (C   F   Am   G) omzetten naar D. We weten dat de progressie I   IV   vi   V is.
We moeten nu uitzoeken welke akkoorden er in de D toonladder zitten.
Volgens de kwintencirkel horen er twee verhogingen (♯) in de toonladder van D, te weten een Cis (C♯) en een Fis (♯).

De volgende stap is dan het uitschrijven van de complete D toonladder, als volgt:

Pakken we nu dezelfde akkoordprogressie uit de D toonladder, die we in de C toonladder hebben gebruikt (I  IV   vi   V), dan hebben we de getransponeerde akkoordprogressie in de D toonladder gevonden.

Transponeren door ½ stappen te tellen

Zelfs zonder een gedegen kennis van muziektheorie, is het met behulp van het "tellen" van de noten in een toonladder, mogelijk om naar een andere toonladder te switchen. Stel dat we van de C toonladder naar de G toonladder willen transponeren, en we hebben de akkoordprogressie C F G in de C toonladder.
Schrijf de C toonladder uit met al zijn halve stappen, en zoals je weet, is iedere fret op de gitaarhals een ½ stap. Dat ziet er als volgt uit:

Als je van de toonsoort C naar de toonsoort G wilt, begin je te tellen. Je ziet in de afbeelding hierboven dat er 7 halve stappen zijn van C naar G, als volgt:
C naar C♯ = ½ stap = 1 fret
C♯ naar D = ½ stap = 1 fret
D naar D♯ = ½ stap = 1 fret
D♯ naar E = ½ stap = 1 fret
E naar F = ½ stap = 1 fret
F naar F♯ = ½ stap = 1 fret
F♯ naar G = ½ stap = 1 fret

Om dus van het akkoord C naar G te gaan, hebben we 7 stappen nodig.
Als we het F akkoord willen transponeren moeten we weer 7 halve stappen tellen vanaf F, en dan kom je uit bij C (F F♯ G G♯ A A♯ B C).
Als we het G akkoord willen transponeren moeten we weer 7 halve stappen tellen vanaf G, en is het getransponeerde akkoord een D (G G♯ A A♯ B C C♯ D).

En daarmee is de akkoordenprogressie uit C F G uit de toonladder C omgezet naar de akkoordenprogressie G C D uit de toonladder G, en is het transponeren succesvol afgesloten.

Transponeren met een Capo

Eerst willen we het gebruik van Barré akkoorden aanstippen, waarvoor we verwijzen naar het website onderdeel "Akkoorden theorie".
Barré akkoorden zijn vaak lastig te spelen, maar ze geven de gitarist bijna onbeperkte mogelijkheden om heel snel van akkoorden in de ene toonladder, naar akkoorden in de andere toonladder te switchen. Een Barré akkoord in F wordt simpelweg een Barré akkoord in G door 1 hele stap (= 2 fretten) op de gitaarhals naar boven te schuiven.

De snelle en eenvoudige oplossing is, zeker als je Barré akkoorden lastig vindt spelen, het gebruik maken van een Capo, ook wel Capotasto genoemd (Capotasto betekent oorspronkelijk topkam). Een Capo is een klem die je op je gitaar kunt zetten om de snaren hoger te laten klinken. Je verplaatst als het ware de topkam, wat de naam verklaart.
Als je de Capo bijvoorbeeld bevestigt bij de tweede fret, dan maak je daarmee de snaren eigenlijk korter en klinken alle snaren een hele toon (2 fretten = 2 ½ stappen = 1 hele toon) hoger.

Als je de akkoordenprogressie G C D als uitgangspunt neemt, en je zou de akkoordenprogressie in A willen spelen, dan zou je de grondtoon G twee ½ stappen moeten opschuiven op de gitaarhals, om het akkoord in A te spelen (G G♯ A).

Wat je simpelweg doet is je Barré vinger (de wijsvinger) vervangen door een Capo. Dat geeft je als gitarist de mogelijkheid om de moeilijke Barré akkoorden te omzeilen, en het geeft je meer vrijheid om ingewikkelder akkoorden te zetten, omdat je de wijsvinger niet meer nodig hebt om alle snaren op de tweede fret in te drukken.
In ons voorbeeld speel je, met Capo, dus nog steeds een G akkoord, maar doordat de Capo om de tweede fret is geklemd, is het G akkoord nu een A akkoord geworden. Hetzelfde geldt voor het C akkoord, dat klinkt nu als een D akkoord (C C♯ D), en het D akkoord klinkt nu als een E akkoord (D D♯ E).

Het grappige is, dat je de nieuwe akkoorden ook weer zonder Capo kunt spelen, en dan op de oorspronkelijke manier, dus vanaf de 0 positie, de open snaren positie:

De akkoorden A, D en E klinken dan een octaaf lager, maar hebben precies dezelfde klankkleur als dezelfde akkoorden A, D en E, die met een Capo op de tweede fret worden gespeeld.

Transponeer-tabellen

---

Als het qua theorie allemaal wat teveel voor je wordt, dan kun je wellicht onderstaande tabellen gebruiken. We laten daarin alle majeur en mineur toonladders de revue passeren, zodat je in één oogopslag kunt zien welke noten er in een toonladder zitten, en op welke toontrap. We hebben er ook bij aangegeven of het een majeur of een mineur akkoord is, dat je op een bepaalde noot moet spelen. De eenvoudigste manier om te transponeren!

Wel is het belangrijk dat je weet, dat er een verschil zit tussen de majeur en de mineur toonladders, wanneer je majeur of mineur akkoorden moet gebruiken. Tussen de majeur en mineur toonladders zit ook een verschil in de schrijfwijze van grote en kleine Romeinse cijfers. In het onderstaande overzicht zie je de afwijkende Romeinse cijfers, een klein geschreven Romeins cijfer geeft aan dat er een mineur akkoord gespeeld moet worden, een groot Romeins cijfer dat er een majeur akkoord van toepassing is.
In een simpel overzicht is dit als volgt samen te vatten:

Een voorbeeld voor majeur akkoorden. Stel dat je een muziekstuk schrijft in (of transponeert naar) F majeur, dan zijn de in deze toonladder voorkomende noten: F   G   A   B♭   C   D   E   F. Dat kun je opzoeken in onderstaande tabel met majeur toonladders.
Ga je nu de akkoorden bij deze toonladder maken, dan moeten deze akkoorden respectievelijk zijn:
F   Gm   Am   B♭   C   Dm   Em   F, zie de Romeinse cijfers bij de toontrappen.

Een voorbeeld met een mineur toonladder, stel C mineur, een toonladder met de noten: C   D   E♭   F   G   A♭   B♭   C. Ook dat kun je opzoeken in de onderstaande tabel met mineur toonladders.
Als je akkoorden bij deze mineur toonladder gaat maken, zie je dat de Romeinse cijfers afwijken van die bij de majeur toonladder, er komen dus op andere plaatsen mineur en majeur akkoorden, als volgt:
Cm   Dm   E♭   Fm   Gm   A♭   B♭   Cm.